1.3.4 TRIÁNGULOS SEMEJANTES

SEMEJANZA DE TRIÁNGULOS




SE DICE QUE DOS TRIÁNGULOS SON SEMEJANTES CUAN LA MEDIDA DE SUS ÁNGULOS TIENEN LA MISMA MEDIDA  Y SUS LADOS PUEDEN TENER UNA MEDIDA DIFERENTE.

ejemplo:

teorema de tales de mileto

cuando utilizamos la semejanza de triángulos este teorema tiene una gran importancia para resolver estos triángulos semejantes , el teorema establece que si dos transversales cortan a varias paralelas , determinan en ellas  segmentos correspondientes que sin proporcionales.

TEOREMA DE PITÁGORAS

En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados (llamamos "triángulo rectángulo" a un triángulo con un ángulo recto).

1.3.3 triángulos congruentes

triángulos congruentes

Son aquellas figuras cuyos angulos correspondientes son proporcionales , asi los triángulos semejantes tienen la misma forma  pero no necesariamente la misma magnitud.

SE DENOTAN CON ESTOS SÍMBOLOS:

EJERCICIO:

POSTULADOS DE CONGRUENCIA

PARA DETERMINAR SI UN TRIANGULO ES CONGRUENTE NO ES NECESARIO COMPARAR TODOS SUS ELEMENTOS EXISTEN POSTULADOS LOS CUALES NOS PERMITEN COMPARAR 

Triángulo	Postulados de congruencia
	Postulado LAL (Lado, Ángulo, Lado) Dos triángulos son congruentes si dos lados de uno tienen la misma longitud que los dos lados del otro triángulo, y los ángulos comprendidos entre esos lados tienen también la misma medida.
	Postulado ALA (Ángulo, Lado, Ángulo) Dos triángulos son congruentes si dos ángulos interiores y el lado comprendido entre ellos tienen la misma medida y longitud, respectivamente. (El lado comprendido entre dos ángulos es el lado común a ellos).
	Postulado LLL (Lado, Lado, Lado) Dos triángulos son congruentes si cada lado de un triángulo tiene la misma longitud que los correspondientes del otro triángulo.

EJEMPLOS:

1.3.1 clasificación y propiedades de los triángulos según la medida de sus lados

clasificación y propiedades de los triángulos según la medida de sus lados 

con la medida de sus lados los ángulos se clasifica en:

Triángulo equilátero

Si sus tres lados tienen la misma longitud (los tres ángulos internos miden  grados).

Triángulo isósceles

Si tiene dos lados de la misma longitud. Los ángulos que se oponen a estos lados tienen la misma medida.

 Triángulo escaleno

Si todos sus lados tienen longitudes diferentes. En un triángulo escaleno no hay ángulos con la misma medida.

1.3.2 "clasificación y propiedades de los triángulos según la medida de sus angulos"

"clasificación y propiedades de los triángulos según la medida de sus ángulos"

1- triángulo rectángulo: es aquel que tiene un angulo recto de 90° , los lados que forman el lado angulo recto se les llama catetos y al lado mas grande hipotenusa.

2-triangulo oblicuángulo: es lo contrario de el traingulo rectangulo es que carece de ángulos rectos estos de dividen en:

triangulo acutangulo : son tres ángulos que son agudos:

triangulo obtusangulo:  tiene un angulo obtuso mayor de 90° , pero menor de 180°

rectas y puntos notables de un triangulo:

mediatriz y circuncentro:

mediatriz: es una line perpendicular a un segmento que pasa por el punto medio.

• mediatriz por medio de el compás: 
• utilizar la amplitud del segmento.
• que la amplitud sea mayor a la mitad de un lado.
• marcarlo en cada uno de los vértices del triángulo.

circuncentro: es aquel punto donde se unen  las mediatrices , se le llama así porque es el centro de circunferencia , circunscrita al triángulo es decir la circunferencia que pasa por los tres vértices del triángulo. 

Mediana y baricentro:

mediana: es la linea que pasa por el punto medio de un segmento hasta el vertice del opuesto.

baricentro: es el punto donde se intersectan las medianas , también llamado centro de gravedad, 

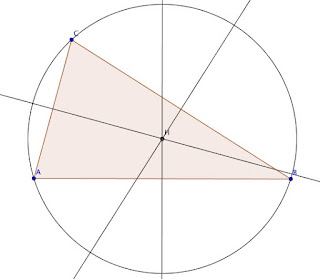
ALTURA Y ORTOCENTRO:

altura: es un segmento que va de el vértice y al lado opuesto y es perpendicular a dicho lado o su prolongación .

ortocentro: es el punto donde se intersectan las tres alturas de un triángulo o sus prolongaciones.

RECTA DE EULER

Es  el baricentro, el ortocentro, y el circuncentro, se puede decir que son los tres puntos colineales es decir una recta pasa por los 3 puntos .

SUMA DE ÁNGULOS INTERNOS DE UN TRIÁNGULO 

En cualquier triangulo la suma de sus angulos internos , forman una angulo llano.

un angulo externo de un triangulo es el complemento del angulo interno., la suma de ellos es de 360°

los ángulos externos tienen la propiedad de ser la suma de los dos ángulos internos no adyacentes a el

EJERCISIOS

1.3 "TRIÁNGULOS"

TRIÁNGULOS:

Es un polígono que tiene 3 lados . el vértice de un triángulo  es el punto en el cual  se juntan sus dos lados. 

el simbolo para denotar un triangulo es: 

un triángulo puede designarse por medio de letras mayúsculas en cualquier orden para sus vértices y se usan minúsculas para los lados :

1.2.4 "ángulos en el plano cartesiano"

ÁNGULOS EN EL PLANO CARTESIANO

Las características de un ángulo orientado en un sistema cartesiano son:

•            Su vértice coincide con el origen de coordenadas.
• ·           Está generado por la rotación de una semirrecta con origen en (0;0). La semirrecta parte desde una posición inicial coincidente  con el semieje positivo de las x y gira manteniendo fijo su origen hasta llegar a una posición que marca su lado terminal.
• ·           El ángulo es positivo cuando está generado en sentido contrario al movimiento de las agujas del reloj y negativo cuando está generado en sentido horario.
• ·          La rotación de la semirrecta puede ser mayor que un giro.

Se considera al plano cartesiano dividido en cuatro sectores llamados cuadrantes:

Se determina en cuál de los cuadrantes se encuentra el lado terminal del ángulo y esta posición  da la ubicación del ángulo. El lado terminal de los tres ángulos representados está en el primer cuadrante por  lo que todos ellos pertenecen a dicho  cuadrante.

1.2.3 CLASIFICACIÓN DE LOS ÁNGULOS

CLASIFICACIÓN DE LOS ÁNGULOS

sistema cíclico:

En el sistema cíclico el ángulo unidad es el radián (rad) que es un ángulo con vértice en el centro de una circunferencia y cuyos lados abarcan un arco de longitud igual al radio de la circunferencia.

los ángulos han recibido una clasificación de acuerdo a la abertura que tienen reciben nombres específicos:

si dos rectas perpendiculares al momento de cortarse forman ángulos rectos , la condicion de proporcionalidad se denota con el símbolo I

CLASIFICACIÓN DE LOS ÁNGULOS POR PAREJAS:

Ángulos consecutivos son aquellos que tienen el vértice y un lado común.

Ángulos complementarios:

Dos ángulos son complementarios si suman 90°.

Ángulos suplementarios: Dos ángulos son suplementarios si suman 180°.

ángulos conjugados: son aquellos que suman 360°

EJERCICIOS

Ángulos adyacentes: son dos ángulos consecutivos. tal que dos lados no son colineales, suman 180°

Ángulos opuestos por el vértice cuando los lados de uno son semirrectas contrarias a los lados del otro. Los ángulos opuestos al vértice tienen como propiedad que“todos los ángulos opuestos por el vértice son iguales”.

ÁNGULOS FORMADOS POR DOS PARALELAS Y UNA TRANSVERSAL;

Dos rectas son paralelas si, estando en un plano, no se cortan, la condicion del paralelismo se denota:  ||

En una recta que se corta dos o mas paralelas se le da el nombre de transversal .

Al cortarse las rectas se forman ángulos los cuales se clasifican en pareja de la siguiente manera:

  Ángulos correspondientes

      Son los que están al mismo lado de las paralelas y al mismo lado de la transversal son los ángulos que se ubican en las esquinas correspondientes y valen lo mismo.

Ángulos alternos externos

   Son los que "fuera" de las paralelas a distinto lado de ellas y a distinto lado de la transversal. Son iguales entre sí; es decir miden lo mismo.

Ángulos alternos internos

      Son los que están entre las paralelas a distinto lado de ellas y a distinto lado de la transversal. Son iguales entre sí; es decir miden lo mismo.

ejercicios